What is an Kirchhoff's First Law and Kirchhoff's Second Law

In the lumped element model of electrical circuits, Kirchhoff’s Laws, often known as circuit laws, are two mathematical equality equations that deal with electricity, current, and voltage (potential difference).
These laws are regarded as corollaries of the Maxwell equations for the low-frequency limit for alternating current (AC) circuits and were first proposed by the German physicist Gustav Kirchhoff in 1845. Direct current (DC) circuits can be accurately modeled using the equations.
Kirchhoff’s Voltage Law and Kirchhoff’s Laws For Current And Voltage are other names for Kirchhoff’s Laws.
If we know the values of the electrical components inside a closed circuit, we may use Kirchhoff’s circuit law, which relates to the junction rule and his closed-loop rule, to calculate and determine the currents and voltages around any closed circuit.

Sometimes it is impossible to determine the voltages or currents flowing across a circuit using only Ohm’s Law, such as in bridge or T networks. Kirchhoff’s Circuit Law can be used to obtain the circuit equations that are necessary for these kinds of calculations.

Kirchhoff’s First Law – The Current Law, (KCL)

According to Kirchhoff’s Current Law (KCL), “the total current or charge entering a junction or node is exactly equal to the charge exiting the node as it has nowhere else to go, as no charge is wasted within the node.” In other words, I(exiting) + I(entering) = 0; the algebraic sum of ALL currents entering and leaving a node must be equal to zero. Kirchhoff’s theory is frequently referred to as the conservation of charge.

In this case, I1, I2, and I3 are the three currents entering the node, and I4 and I5 are the two currents exiting the node. Consequently, the equation can also be rewritten as;I1 + I2 + I3 – I4 – I5 = 0
A link or junction of two or more current-carrying elements, such as cables and components, is referred to as a node in an electrical circuit. A closed circuit channel is also necessary for current to pass through a node, either in or out. When analyzing parallel circuits, we can make use of Kirchhoff’s current law.

According to Kirchhoff’s Voltage Law (KVL), “in any closed loop network, the total voltage around the loop is equal to the sum of all the voltage drops within the same loop,” which is also equal to zero. In other words, all of the voltages inside the loop’s algebraic total must be zero. Kirchhoff’s theory is referred to as the Conservation of Energy.

Regardless of where you start in the loop, keep going in the same way while noting the direction in which each voltage drop, whether positive or negative, occurs before going back to where you started. Maintaining the same direction—clockwise or counterclockwise—is crucial to ensure that the voltage sum at the end is zero. Kirchhoff’s voltage law can be used to analyze series circuits.
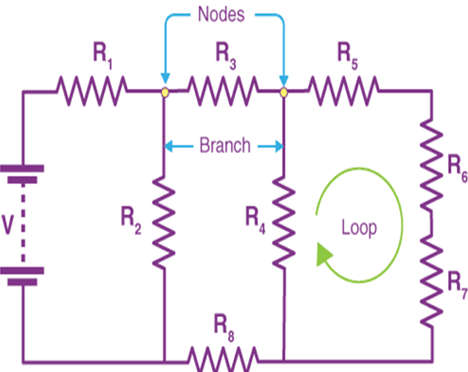
Kirchhoff’s Circuit Laws can be used to analyze both DC and AC circuits, and a variety of terms and terminology are used to characterize the various circuit components, including nodes, pathways, branches, loops, and meshes. Since these words are commonly used in circuit analysis, it is crucial to comprehend them.

Example: Bridge Circuit

Electronics frequently use bridge circuits. They are utilized in switching circuits, transducers, and measurements. A bridge circuit is shown below. We will demonstrate how to use Kirchhoff’s principles to calculate the cross current I5 in this case. Resistors R1 through R4 are used in the circuit’s four bridge sections. With resistor R5, there is a single cross-bridge connection. The voltage V and current I applied to the bridge are both constant.
According to the first Kirchhoff law (KCL), a node’s total currents are equal to zero. As a result of this:
I = I1 + I2I = I3 + I4

I = I3 + I5
According to the second Kirchhoff law (KVL), the total voltage across all of the loop’s components is zero. As a result of this:R1I1 + R3I3 − V = 0
R1I1 + R5I5 − R2I2 = 0

R3I3 − R4I4 − R5I5 = 0
The expression for I5 (the current in the cross branch) can be found by rewriting the six sets of equations above using standard algebra:I5=V(R2R3−R1R4)/R5(R1+R3)(R2+R4)+R1R3(R2+R4)+R2R4(R1+R3)
According to the equation, the bridge must be balanced with a bridge current of zero for this to happen:R2R3=R1R4